Manual of Method for Calculating Primary Energy Consumptions under 2016 Building Energy Code (Non-residential Buildings)

National Institute for Land and Infrastructure Management (NILIM), Ministry of Land, Infrastructure and Building Research Institute (BRI), Transport and Tourism, National Research and Development Agency

8. Evaluation Method of Cogeneration System

This chapter shows the logic for calculating the primary energy consumptions of cogeneration systems.

8.1 Introduction

8.1.1 Scope of Application

The cogeneration systems that should be evaluated for calculation are defined below.

Gas-type cogeneration system whose waste heat is discharged with hot water
- A gas-type cogeneration system whose waste heat is removed by steam can be deemed to be that whose waste heat is removed by hot water, and evaluated for calculation.
- Gas turbines, fuel cells, and diesel engines are not inputted for calculation.
In the case of installation several cogeneration systems, those with the same type and the same generation power.
- In the case where several cogeneration systems with different generation outputs are mixed, the number of installed cogeneration systems can be inputted, an averaged generation output be inputted in the item of Generation output (on the assumption that several cogeneration systems with the same generation output are introduced). In addition, generation and heat exhaust efficiencies are weighted by a rated generation output of each cogeneration system, and averaged. The result of the calculation can be inputted.
Cogeneration system that supplies electricity and heat to the same system
- In the case where electricity and heat are supplied to several systems, one representative system can be selected, and only a cogeneration system that supplies electricity and heat can be inputted.
  - The system that has the largest total of a rated cooling capacity (kW) of heat source equipment that produces cold energy by using exhaust heat from a cogeneration system, and a rated cooling capacity (kW) of a water heater included in the same system as the cogeneration system, is assumed to be a representative system.
Cogeneration system that self-consumes generated power and heat
- In the case where generated power and waste heat are externally supplied from a cogeneration system, the relevant system can be evaluated as a system self-consuming all of them (self-consumed generated power and waste heat are calculated on the assumption that a generation is controlled to a power demand or lower, and excessive waste heat is dissipated).
Cogeneration system whose operation based an electricity demand is controlled
- In the case where a cogeneration system is operated based on a heat demand, the relevant system’s operation can be deemed to be an operation based an electricity demand.
Cogeneration system whose waste heat use is evaluated concerning primary energy consumption performance under the Building Energy Code
- In the case where waste heat from a cogeneration system is supplied to a facility using the heat to melt snow, protect freezing or heat circulated water (public bathhouse or heated swimming pool), a facility using non-portable water (dishwasher, washing machine, etc.) or other similar installation that is not covered by evaluation of energy consumption performance, the relevant cogeneration system can be evaluated on the assumption that its waste heat is not supplied to these facilities.

8.1.2 Normative Reference and Literatures

[1] JIS B 8122:2009 Test methods for measuring performance of cogeneration system
[2] JIS B 8622:2009 Absorption refrigerating machines
[3]Sumiyoshi Laboratory, Sustainable Building Energy Systems
Faculty of Human-Environment Studies, Kyushu University and Jyukankyo Research Institute Inc.: 2019 review and survey report concerning sophistication of method for evaluating performance of commercial cogeneration systems under the project to promote the development or revision of building standards, March 2018
The Society of Heating, Air-Conditioning and Sanitary Engineers of Japan: Handbook of air-conditioning and sanitary engineering 14th edition (Chapter 17 “Table 17.6 Insulation thickness of pipe” of 5 Planning, Execution and Maintenance Title, referenced), April 2010
[5]Editorial Committee for Manual of 2013 Building Energy Code for Houses and Buildings: Method and Manual of Calculation and Judgment Conforming to the 2013 Building Energy Code, I, Non-residential Buildings (Part II Chapter 4 “Table 2.4.2 Heat loss coefficient of pipe,” referenced), National Institute for Land and Infrastructure Management (NILIM), Ministry of Land, Infrastructure and Building Research Institute (BRI), Transport and Tourism, National Research and Development Agency, May 2013
The Society of Heating, Air-Conditioning and Sanitary Engineers of Japan: City gas cogeneration evaluation program―CASCADEⅢ Ver.3.2―, July 2013

8.1.3 Definition of Terms

CGS

This refers to the body of a commercial cogeneration system.
Rated generation output of CGS

This refers to the power generation during rated operation of a CGS (based performance test methods that are specified in JIS B 8122).
Power generation efficiency of CGS (rated operation, loading factor 0.75 h, loading factor 0.50 h)

This refers to the power generation efficiency of a CGS under specified loading conditions for CGS (rated operation, loading factor 0.75 h, loading factor 0.50 h) (based performance test methods that are specified in JIS B 8122).
Recovery efficiency of waste heat from CGS (rated operation, loading factor 0.75 h, loading factor 0.50 h)

This refers to the waste heat recovery efficiency of a CGS (rated operation, loading factor 0.75 h, loading factor 0.50 h ) under specified loading conditions for the CGS (rated operation, loading factor 0.75 h, loading factor 0.50 h) (based performance test methods that are specified in JIS B 8122).
Priority of waste heat use

This refers to the order in which waste heat is charged into each of a heater, an air conditioner and a water heater (1st, 2nd or 3rd place, or no charge).
Absorption chiller/heater with auxiliary waste heat recovery

This is an absorption hot and chilled water generator (refrigerator) that uses waste heat of a CGS as a part of heat source for manufacturing of　refrigerants.
CGS’s auxiliary power

This refers to the power consumptions of auxiliary machines such as body control panel and heat dissipation fan, and those of a hot water circulating pump, a cooling tower pump, heater and other similar device.
CGS’s auxiliary power ratio

This refers to a ratio of CSG’s auxiliary power to its power generation.
COP at use of waste heat from absorption chiller/heater with auxiliary waste heat recovery

This is an coefficient of performance (COP) of a absorption chiller/heater with auxiliary waste heat recovery when the equipment is operated only with waste heat to be charged.
\( \frac{ \mbox{ Refrigerating capacity [kW]} }{ \mbox{Waste heat charge [kW]} } \)
*Maximum share rate of power load of CGS

In the case where a building’s electricity is covered by power generated from a CGS, of an accumulated daily power consumption in the building, this refers to a rate of power load that can be supplied by the CGS after the output of the CGS is controlled in terms of protection of a reverse power flow etc.
Maximum operation time of CGS

This refers to the daily maximum operation time of a CGS in the case of its intermittent operation.
Average power ratio between operation and non-operation hours of building

This refers to a ratio between average power consumptions during hours of operation and non-operation of a building.
Correction of generation efficiency

This refers to a correction value for a power generation efficiency in an equipment catalog (measured value based on the performance test methods that are specified in JIS B 8122).
Heat loss rate of waste heat

Of waste heat from a CGS, this refers to a rate of waste heat that can be used with the exclusion of a heat quantity discharged from the surface of a pipe etc.
Availability rate of waste heat of absorption chiller/heater with auxiliary waste heat recovery

This refers to a rate of waste heat that can cover a part of a primary energy consumption of an absorption chiller/heater with auxiliary waste heat recovery.
Available waste heat

This refers to a maximum amount of waste heat that can be used in waste heat utilization equipment (a heater, an air conditioner or a water heater) in the case where waste heat is sufficiently acquired.
Load factor

Loading factors of a CGS and an absorption hot and chilled water generator of waste heat charge type are defined below.
CGS: \( \frac{\mbox{Generation output[kW]}}{\mbox{Rated generation output[kW]}}\)
Absorption chiller/heater with auxiliary waste heat recovery: \( \frac{\mbox{Treated heat quantity [kW]}}{\mbox{Rated cooling capacityl[kW]}} \)
Effective power generation

This refers to a CGS’s power generation that excludes its auxiliary power.
Effective waste heat recovery

Of an amount of waste heat recovered from a CGS, this refers to the sum of heat quantities that are consumed by waste heat utilization equipment.
Waste heat usage

This refers to an amount of waste heat that is used in waste heat utilization equipment (a heater, an air conditioner or a water heater).

8.1.4 Calculation Flow

In order to create this calculation method, the cogeneration evaluation program CASCADEⅢ was developed to a method to calculate energy consumptions based on daily loading data, and parameters etc. used to evaluate actual work performance were added to this method.

A flow of evaluation is shown in the following diagram. The daily calculation results of power consumptions, heating and hot-water supply loads and other information are obtained from the main body of the energy consumption performance program. Based on these results, the operation status of a CGS is determined. In the main body of the program, the energy consumptions of electric power, cooling, heating and hot-water supply are calculated on the assumption that electric power or waste heat is not acquired from the CGS. In this program, the primary energy consumptions that can be reduced in the items of electric power, cooling, heating and hot-water supply, and the gas consumption of a CGS are calculated. Finally, the gas consumption of CGS is deducted from the energy consumptions of electric power, cooling, heating and hot-water supply that are calculated in the main body of the program, and then, the energy consumption of the whole building can be calculated in consideration of the increment of the gas consumption of CGS.

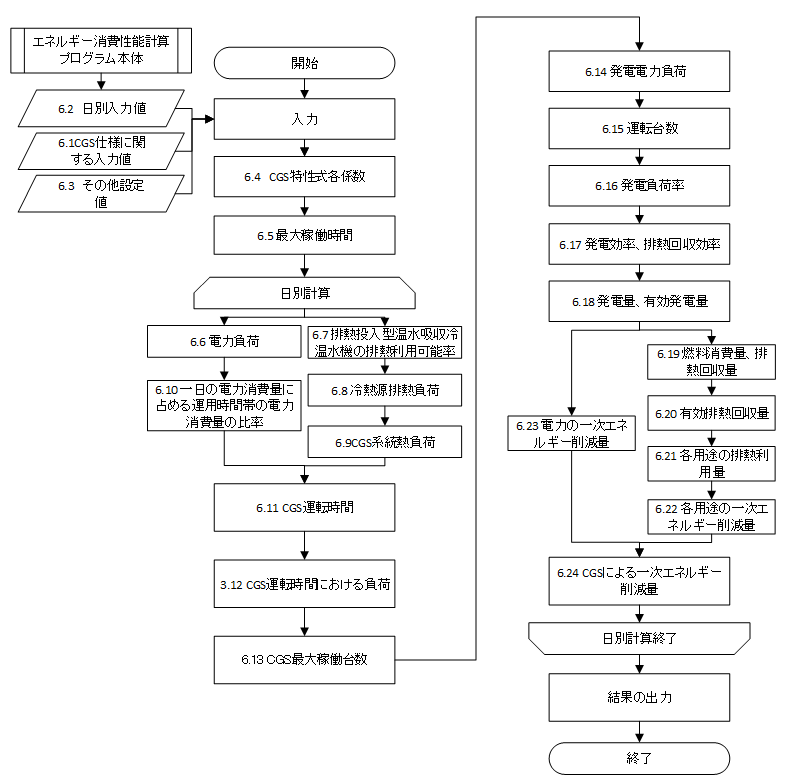
Figure 1. Flow of evaluation

8.1.5 Input Value

8.1.5.1 Input value for CGS specifications

The list of set values for CSG and the absorption chiller/heater with auxiliary waste heat recovery that are inputted in the program are shown in the following table.

Table 1. Input
Variable name	Description	Unit	Reference
\(E_{cgs,rated}\)	Rated generation output of CGS	kW	Form 7-3
\(N_\{cgs}\)	Number of installed CGSs	Number	Form 7-3
\(f_{cgs,e,rated}\)	Rated power generation efficiency of CGS (Lower heating value standard)	Non-dimensional	Form 7-3
\(f_{cgs,e,75}\)	Power generation efficiency of CGS at loading factor 0.75 (Lower heating value standard)	Non-dimensional	Form 7-3
\(f_{cgs,e,50}\)	Power generation efficiency of CGS at loading factor 0.50 (Lower heating value standard)	Non-dimensional	Form 7-3
\(f_{cgs,hr,rated}\)	Rated heat exhaust efficiency of CGS (Lower heating value standard)	Non-dimensional	Form 7-3
\(f_{cgs,hr,75}\)	Heat exhaust efficiency of CGS at loading factor 0.75 (Lower heating value standard)	Non-dimensional	Form 7-3
\(f_{cgs,hr,50}\)	Heat exhaust efficiency of CGS at loading factor 0.50 (Lower heating value standard)	Non-dimensional	Form 7-3
\(n_{pri,hr,c}\)	Priority of waste heat use (cooling source) *1	Non-dimensional	Form 7-3
\(n_{pri,hr,h}\)	Priority of waste heat use (heat source) *1	Non-dimensional	Form 7-3
\(n_{pri,hr,W}\)	Priority of waste heat use (hot-water supply) *1	Non-dimensional	Form 7-3
\(C_\{24ope}\)	Presence or absence of CSG 24-hour operation (Yes/NO)	-	Form 7-3
\(q_{AC,link,c,j,rated}\)	Rated cooling capacity of absorption chiller/heater with auxiliary waste heat recovery	kW/unit	Form 7-3
\(E_{AC,link,c,j,rated}\)	Rated consumption energy of a main module of an absorption chiller/heater with auxiliary waste heat recovery	kW/unit	Form 7-3
\(N_{AC,ref,link}\)	Number of absorption chillers/heaters with auxiliary waste heat recovery in a system allowing for the use of waste heat of CGS	Number	Form 7-3

Integer from 0 to 3 In the case where a column in the input sheet is blank, the value of an integer is assumed to be “0.” This means that waste heat is not used for the targeted purposes. One of \(n_{pri,hr,c}\), \(n_{pri,hr,h}\) and \(n_{pri,hr,W}\) must be “1.”

8.1.5.2 Input value by day (Read of results calculated for other systems）

Based on the results calculated for other systems, read the following values. The method for calculating these values is shown in Annex G.10

Table 2. Input
Variable name	Description	Unit	Remarks
\(E_{AC,total,d}\)	Power consumption of air conditioning equipment at date	MWh/day	*1
\(E_{AC,ref,c,d}\)	Primary energy consumption of a cooling source module of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat from CGS, at date d (total of primary energy consumptions of several cooling sources)	MJ/day	*2
\(mxL_{AC,ref,c,d}\)	Loading factor of a cooling source of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date d (Loading factors of several cooling sources are divided in proportion to their rated cooling capacities.)	Non-dimensional	*2
\(E_{AC,ref,h,hr,d}\)	Primary energy consumption of a main module of a heat source group allowing for the use of waste heat of CGS, at date d (total of primary energy consumptions of several heat sources)	MJ/day	*2
\(q_{AC,ref,h,hr,d}\)	Heating load of a heat source group allowing for the use of waste heat of CGS, at date d (total of heating loads of several heat source groups)	MJ/day	*2
\(E_{V,total,d}\)	Power consumption of air conditioning system at date	MWh/day	*3
\(E_{L,total,d}\)	Power consumption of lighting installation at date	MWh/day	*4
\(E_{W,total,d}\)	Power consumption of hot-water supply system at date	MWh/day	*5
\(E_{W,hr,d}\)	Primary energy consumption of a water heater (system) allowing for the use of waste heat of CGS, at date d (total of primary energy consumptions of water heaters)	MJ/day	*5
\(q_{W,hr,d}\)	Supply load of a water heater (system) allowing for the use of waste heat of CGS, at date d (total of supply loads of several water heaters)	MJ/day	*5
\(E_{EV,total,d}\)	Power consumption of hot-water supply system at date	MWh/day	*6
\(E_{PV,total,d}\)	Power generation of system with effective use of energy (solar power generation system) at date	MWh/day	*7
\(E_{M,total,d}\)	Power consumption of other system at date	MWh/day	*8
\(T_{AC,c,d}\)	Operation time of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date d (The largest among operation times of several cooing sources is employed.)	h/day	*2
\(T_{AC,h,d}\)	Operation time of an heat source group allowing for the use of waste heat of CGS, at date d (The largest among operation times of several heat sources is employed.)	h/day	*2
\(f_\{eopeHi}\)	Average power ratio between operation and non-operation hours of building	Non-dimensional	*8

*1 Calculation result of air conditioning equipment Sum of power consumptions of a total heat exchanger, heat source main module, heat source auxiliary module, primary pump, cooling tower fan and cooling tower pump
*2 Calculation result of air conditioning equipment
*3 Calculation result of mechanical ventilation equipment
*4 Calculation result of lighting installation
*5 Calculation result of hot-water supply system
*6 Calculation result of elevator
*7 Calculation result of system with effective use of energy (solar power generation system)
*8 Calculation result of other system Value calculated from equipment heat generation in each room

8.1.6 Constant

The common constants that are used in this chapter is shown below.

Table 3. Input
Variable name	Description	Unit	Value
\(f_\{eopeMn}\)	Required power ratio for operation judgment standard	Non-dimensional	0.5
\(f_\{hopeMn}\)	Required waste heat ratio for operation judgment standard	Non-dimensional	0.5
\(f_{esub,cgswc}\)	CGS’s auxiliary power ratio (in the presence of a cooling tower)	Non-dimensional	0.06
\(f_{esub,cgsac}\)	CGS’s auxiliary power ratio (in the absence of a cooling tower)	Non-dimensional	0.05
\(f_\{lh}\)	Ratio of lower to higher heating value of gas	Non-dimensional	0.90222
\(f_{prime,e}\)	Primary energy conversion coefficient of electricity	MJ/kWh	9.76
\(f_{COP,link,hr}\)	COP at use of waste heat from absorption chiller/heater with auxiliary waste heat recovery	Non-dimensional	0.75
\(f_\{elmax}\)	Maximum share rate of power load of CGS	Non-dimensional	0.95
\(T_\{STn}\)	Maximum operation time of CGS	h/day	14
\(T_{STmin,W}\)	Minimum operation time of CGS when waste heat is used only for hot-water supply	h/day	10
\(f_{cgs,e,cor}\)	Correction of generation efficiency	Non-dimensional	0.99
\(f_{hr,loss}\)	Heat loss rate of waste heat	Non-dimensional	0.97

8.2 Calculation of CGS Energy Consumption Characteristic

Determine each different coefficient to calculate a CGS’s energy consumption characteristic from power generation and heat exhaust efficiency inputs.

Table 4. Input
Variable name	Description	Unit	Reference
\(f_{ cgs, e, rated }\)	Rated power generation efficiency of CGS (Lower heating value standard)	-	Form 7-3: ④ Power generation efficiency at loading factor 1.00
\(f_{ cgs, e, 75 }\)	Power generation efficiency of CGS at loading factor 0.75 (Lower heating value standard)	-	Form 7-3: ⑤ Power generation efficiency at loading factor 0.75
\(f_{ cgs, e, 50 }\)	Power generation efficiency of CGS at loading factor 0.5 (Lower heating value standard)	-	Form 7-3: ⑥ Power generation efficiency at loading factor 0.50
\(f_{ cgs, hr, rated }\)	Rated heat exhaust efficiency of CGS (Lower heating value standard)	-	Form 7-3: ⑦ Heat exhaust efficiency at loading factor 1.00
\(f_{ cgs, hr, 75 }\)	Heat exhaust efficiency of CGS at loading factor 0.75 (Lower heating value standard)	-	Form 7-3: ⑧ Heat exhaust efficiency at loading factor 0.75
\(f_{ cgs, hr, 50 }\)	Heat exhaust efficiency of CGS at loading factor 0.5 (Lower heating value standard)	-	Form 7-3: ⑨ Heat exhaust efficiency at loading factor 0.50

Table 5. Output
Variable name	Description	Unit	References
\(f_{ e2 }\)	Coefficient and term of quadratic formula of CGS’s power generation efficiency characteristic expression	-	8.15
\(f_{ e1 }\)	Coefficient and term of linear formula of CGS’s power generation efficiency characteristic expression	-	8.15
\(f_{ e0 }\)	Coefficient and term of CGS’s power generation efficiency characteristic expression	-	8.15
\(f_{ hr2 }\)	Coefficient and term of quadratic formula of CGS’s heat exhaust efficiency characteristic expression	-	8.15
\(f_{ hr1 }\)	Coefficient and term of linear formula of CGS’s heat exhaust efficiency characteristic expression	-	8.15
\(f_{ hr0 }\)	Constant and term of CGS’s heat exhaust efficiency characteristic expression	-	8.15

Determine \(f_{ e2 }\) ,\(f_{ e1 }\) ,\(f_{ e0 }\) ,\(f_{ hr2 }\) ,\(f_{ hr1 }\) and \(f_{ hr0 }\) from the following formula, using the Lagrange interpolation formula.

\[\begin{eqnarray} f_{ e2 } &=& 8 \times ( f_{ cgs, e,rated } - 2 \times f_{ cgs, e, 75 } + f_{ cgs, e, 50 } ) \\ f_{ e1 } &=& -2 \times ( 5 \times f_{ cgs, e,rated } - 12 \times f_{ cgs, e, 75 } + 7 \times f_{ cgs, e, 50 } ) \\ f_{ e0 } &=& 3 \times f_{ cgs, e,rated } - 8 \times f_{ cgs, e, 75 } + 6 \times f_{ cgs, e, 50 } \end{eqnarray}\]

\[\begin{eqnarray} f_{ hr2 } &=& 8 \times ( f_{ cgs, e,rated } - 2 \times f_{ cgs, e, 75 } + f_{ cgs, e, 50 } ) \\ f_{ hr1 } &=& -2 \times ( 5 \times f_{ cgs, e,rated } - 12 \times f_{ cgs, e, 75 } + 7 \times f_{ cgs, e, 50 } ) \\ f_{ hr0 } &=& 3 \times f_{ cgs, e,rated } - 8 \times f_{ cgs, e, 75 } + 6 \times f_{ cgs, e, 50 } \end{eqnarray}\]

8.3 Maximum Operation Time

Calculate a maximum operation time of a CGS.

Table 6. Input
Variable name	Description	Unit	Reference
\(C_{ 24ope }\)	Presence or absence of CGS 24-hour operation (Yes/NO)	-	Form 7-3: ⑬ Presence or absence of 24-hour operation
\(T_{ STn }\)	Maximum operation time of CGS in the case of intermittent operation.	h/day	G.4

Table 7. Output
Variable name	Description	Unit	References
\(T_{ ST }\)	Maximum operation time of CGS	h/day	8.7、8.8、8.9、8.10

A maximum operation time of CGS, \(T_{ ST }\), is assumed to be \(T_{ STn }\) regardless of building uses. In the presence of \(C_{ 24ope }\), however, the maximum operation time is assumed to be 24.

\[T_{ ST } = \begin{cases} T_{ STn } & , C_{ 24ope } = \mbox{Absence} \\ 24 & , C_{ 24ope } = \mbox{Presence} \end{cases}\]

8.4 Power Loads

Calculate power loads.

Table 8. Input
Variable name	Description	Unit	Reference
\(E_{ AC, total, d }\)	Power consumption of air conditioning equipment at date	MWh/day	8.1.5.2
\(E_{ V, total, d }\)	Power consumption of air conditioning system at date	MWh/day	8.1.5.2
\(E_{ L, total, d }\)	Power consumption of lighting installation at date	MWh/day	8.1.5.2
\(E_{ W, total, d }\)	Power consumption of hot-water supply system at date	MWh/day	8.1.5.2
\(E_{ EV, total, d }\)	Power consumption of hot-water supply system at date	MWh/day	8.1.5.2
\(E_{ M, total, d }\)	Power consumption of other system at date	MWh/day	8.1.5.2
\(E_{ PV, total, d }\)	Power generation of system with effective use of energy (solar power generation system) at date	MWh/day	8.1.5.2

Table 9. Output
Variable name	Description	Unit	References
\(E_{ e, total, d }\)	Power consumption of building at date	kWh/day	8.9、8.10

\[\begin{split} E_{ e, total, d } &= ( E_{ AC, total, d } + E_{ V, total, d } + E_{ L, total, d } \\ & \quad + E_{ W, total, d } + E_{ EV, total, d } + E_{ M, total, d } \\ & \quad - E_{ PV, total, d } ) \times 1000 \end{split}\]

8.5 Availability Rate of Waste Heat of Absorption Chiller/Heater with Auxiliary Waste Heat recovery

Calculate an availability rate of waste heat of an absorption chiller/heater with auxiliary waste heat recovery.

Table 10. Input
Variable name	Description	Unit	Reference
\(mxL_{ AC, ref, c, d }\)	Load factor of a cooling source of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	-	8.1.5.2
\(f_{ link, rated, b }\)	Availability rate of waste heat of absorption chiller/heater with auxiliary waste heat system recovery during its rated operation	-	G.8
\(f_{ link, min, b }\)	Maximum loading factor at which a waste heat of absorption chiller/heater with auxiliary waste heat system recovery can operate only by waste heat	-	G.8
\(f_{ link, down }\)	Rate of reduction of available waste heat by waste heat temperature	-	G.9

Table 11. Output
Variable name	Description	Unit	References
\(f_{ link, d }\)	Availability rate of waste heat of absorption chiller/heater with auxiliary waste heat recovery at date	-	8.6

After determining a rate of available waste heat during rated operation of an absorption chiller/heater with auxiliary waste heat system recovery in consideration of a decline of the relevant rate that is caused by a temperature of heat exhaust, \(f_{ link, rated }\), and a maximum load factor of the absorption chiller/heater when it can operate with the use of only waste heat, \(f_{ link, min }\), calculate a rate of available waste heat for the absorption chiller/heater, \(f_{ link, d }\).

\[f_{ link, rated } = f_{ link, rated, b } \times ( 1 - f_{ link, down } )\]

\[f_{ link, min } = f_{ link, min, b } - ( f_{ link, rated, b } - f_{ link, rated } )\]

\[f_{ link, d } = \begin{cases} 1 & , mxL_{ AC, ref, c, d } < f_{ link, min } \\ 1 - \frac{ mxL_{ AC, ref, c, d } - \left\{ \frac{ f_{ link, rated } - f_{ link, min } }{ 1 - f_{ link, min } } \times mxL_{ AC, ref, c, d } + \left( f_{ link, rated } - \frac{ f_{ link, rated } - f_{ link, min } }{ 1 - f_{ link, min } } \right) \right\} }{ mxL_{ AC, ref, c, d } } & , mxL_{ AC, ref, c, d } \geqq f_{ link, min } \end{cases}\]

Rate of available waste heat for absorption chiller/heater with auxiliary waste heat recovery

The rate of available waste heat for an absorption chiller/heater with auxiliary waste heat recovery represents an amount of energy that can be replaced with waste heat, of input energy required for production of a cooling source in each operation load factor. The rate of available waste heat for the absorption chiller/heater with auxiliary waste heat recovery according to each load factor is shown in the following figure. The absorption chiller/heater can produce cooling sources with the use of only waste heat in the range of low loads, but in the range of high loads, it becomes necessary to charge gas etc. into the machine due to the reduction of the relevant rate.

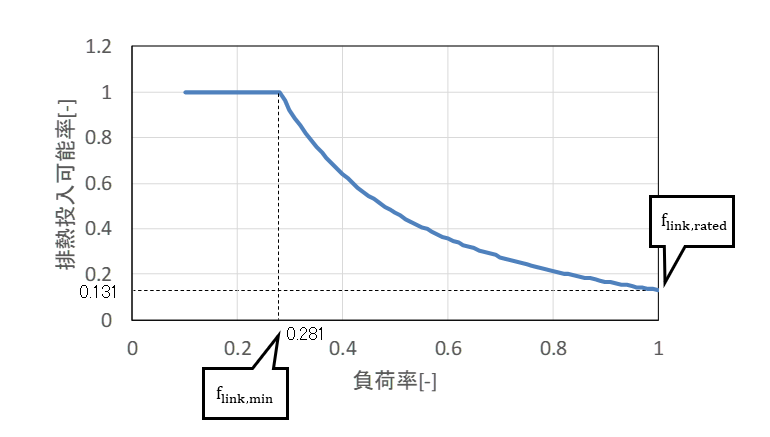
Figure 2. Rate of available waste heat for the absorption chiller/heater with auxiliary waste heat recovery according to each load factor

8.6 Heat Exhaust Load of Cooling Source

Calculate a heat exhaust load of a cooling source.

Table 12. Input
Variable name	Description	Unit	Reference
\(E_{ AC, ref, c, d }\)	Primary energy consumption of a cooling source main module of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	MJ/day	8.1.5.2
\(f_{ link, d }\)	Availability rate of waste heat of absorption chiller/heater with auxiliary waste heat recovery at date	-	8.5
\(q_{ AC, link, c, j, rated }\)	Rated cooling capacity of absorption chiller/heater with auxiliary waste heat recovery	kW/unit	Form 2-5: ⑩ Rated cooling capacity
\(E_{ AC, link, c, j, rated }\)	Rated consumption energy of a main module of an absorption chiller/heater with auxiliary waste heat recovery	kW/unit	Form 2-5: ⑪ Rated energy consumption of main module
\(N_{ AC, ref, link }\)	Number of absorption chillers/heaters with auxiliary waste heat recovery in a system allowing for the use of waste heat of CGS	Number	Form 2-5: ⑧ Number of devices
\(n_{ pri, hr, c }\)	Priority of waste heat use (cooling source)	-	Form 7-3: ⑩ Priority of waste heat use, air conditioning cooling source
\(f_{ COP, link, hr }\)	COP at use of waste heat from absorption chiller/heater with auxiliary waste heat recovery	-	G.5
\(n_{ pri, hr, c}\)	Priority of waste heat use (cooling source)	Non-dimensional	Form 7-3

Table 13. Output
Variable name	Description	Unit	References
\(q_{ AC, ref, ch, hr, d }\)	Heat exhaust load of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	MJ/day	8.7、8.10
\(E_{ AC, ref, c, hr, d }\)	In the use of waste heat, possible amount of reduction of primary energy consumption of a cooling source main module of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	MJ/day	8.10

\[q_{ AC, ref, c, hr, d } = \begin{cases} 0 & , n_{ pri, hr, c } = 0 \\ E_{ AC, ref, c, d } \times f_{ link, d } \times \frac{ \sum_{ j = 1 }^{ N_{ AC, ref, link } } q_{ AC, link, c, j, rated } }{ \sum_{ j = 1 }^{ N_{ AC, ref, link } } E_{ AC, link, c, j, rated } } \times \frac{ 1 }{ f_{ COP, link, hr } } & , n_{ pri, hr, c } \neq 0 \end{cases}\]

\[E_{ AC, ref, c, hr, d } = \begin{cases} 0 & , n_{ pri, hr, c } = 0 \\ E_{ AC, ref, c, d } \times f_{ link, d } & , n_{ pri, hr, c } \neq 0 \end{cases}\]

(Supplementary document) Detailed manual of formula for cooling source’s heat exhaust load

8.7 Heat Loads of CGS Systems

Calculate heat loads of CGS systems.

Table 14. Input
Variable name	Description	Unit	Reference
\(q_{ AC, ref, c, hr, d }\)	Heat exhaust load of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	MJ/day	8.6
\(q_{ AC, ref, h, hr, d }\)	Heating load of a heat source group allowing for the use of waste heat of CGS, at date	MJ/day	8.1.5.2
\(q_{ W, hr, d }\)	Supply load of a water heater (system) allowing for the use of waste heat of CGS, at date	MJ/day	5.6
\(T_{ AC, c, d }\)	Operation time of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	h/day	8.1.5.2
\(T_{ AC, h, d }\)	Operation time of a heat source group allowing for the use of waste heat of CGS, at date	h/day	8.1.5.2
\(T_{ ST }\)	Maximum operation time of CGS	h/day	8.3

Table 15. Output
Variable name	Description	Unit	References
\(q_{ hr, AC, c, d }\)	Heat exhaust load of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	MJ/day	-
\(q_{ hr, AC, h, d }\)	Heat exhaust load of a heat source group allowing for the use of waste heat of CGS, at date	MJ/day	-
\(q_{ hr, total, d }\)	Heat load of CGS heat exhaust system at date	MJ/day	8.9、8.11

In order to determine a heat load of a CGS heat exhaust system at a date d, \(q_{ hr, total, d }\), heat exhaust loads of cooling and heating sources are determined, and a heat exhaust load of hot-water supply is added to the determined loads. The heat exhaust load of the cooling source is corrected according to the number of hours as indicated below if a daily cooling time of the source is shorter than the maximum operation time of a CGS.

\[q_{ hr, AC, c, d } = \begin{cases} q_{ AC, ref, c, hr, d } \times \frac{ T_{ ST } }{ T_{ AC, c ,d } } & , T_{ AC, c, d } > T_{ ST } \\ q_{ AC, ref, c, hr, d } & , T_{ AC, c, d } \leqq T_{ ST } \end{cases}\]

The heat exhaust load of the heating source is corrected in the same way as that of the cooling source.

\[q_{ hr, AC, h, d } = \begin{cases} q_{ AC, ref, h, hr, d } \times \frac{ T_{ ST } }{ T_{ AC, h ,d } } & , T_{ AC, h, d } > T_{ ST } \\ q_{ AC, ref, h, hr, d } & , T_{ AC, h, d } \leqq T_{ ST } \end{cases}\]

Finally, a hot-water supply load is added to the heat exhaust load of the cooling and heating sources. The sum of the supply load and the exhaust load is a heat load of the CGS heat exhaust system. For reference, it is possible to use the exhaust heat of a CGS for hot-water supply by installing a hot water tank even if generation hours of hot-water supply load are different from operation hours of the CGS. For this reason, the relevant load is not corrected based the operation hours.

\[q_{ hr, total, d } = q_{ hr, AC, c, d } + q_{ hr, AC, h, d } + q_{ W, hr, d }\]

8.8 Ratio between Power Consumption during Operation Hours and Daily Power Consumption

Calculate a ratio between a power consumption during operation hours and daily power consumption.

Table 16. Input
Variable name	Description	Unit	Reference
\(T_{ ST }\)	Maximum operation time of CGS	h/day	8.3
\(f_{ eopeHi }\)	Average power ratio between operation and non-operation hours of building	-	8.1.5.2

Table 17. Output
Variable name	Description	Unit	References
\(f_{ eope, R }\)	Ratio between power consumption during operation hours and daily power consumption	-	-

\[f_{ eope, R } = \frac{ f_{ eopeHi } \times T_{ ST } }{ f_{ eopeHi } \times T_{ ST } + ( 24 - T_{ ST } ) }\]

The above formula is a formula from which a power consumption of a CGS during its operation hours (area of orange part) is determined in comparison with a total of power consumptions in one day as shown in the following figure (total of areas of light blue and orange parts). \(f_{ eopeHi }\) represents an average power consumption of a CGS during its operation hours on the assumption that an average power consumption of the CGS during its non-operation hours is 1. The power consumption of the CGS during its operation hours (area of orange part) is represented as \(f_{ eopeHi } \times T_{ ST }\) while the power consumption of the CGS during its non-operation hours (area of light blue part) is represented as \(( 24 - T_{ ST } ) \times 1 \). Accordingly, the above formula can be obtained.

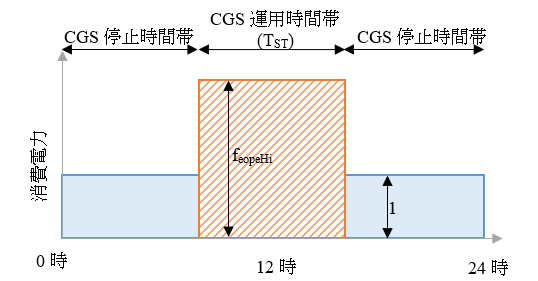
Figure 3. Calculating a CGS’s power consumption during its operation hours that is included in an accumulated daily power consumption

8.9 Operation Time of CGS

Calculate an operation time of CGS.

Table 18. Input
Variable name	Description	Unit	Reference
\(E_{ e, total, d }\)	Power consumption of building at date	kWh/day	8.4
\(q_{ hr, total, d }\)	Heat load of CGS heat exhaust system at date	MJ/day	8.7
\(E_{ cgs, rated }\)	Rated generation output of CGS	kW	8.1.5.1
\(f_{ cgs, e, rated }\)	Rated power generation efficiency of CGS (Lower heating value standard)	-	8.1.5.1
\(f_{ cgs, hr, rated }\)	Rated heat exhaust efficiency of CGS (Lower heating value standard)	-	8.1.5.1
\(f_{ eopeMn }\)	Required power ratio for operation judgment standard	-	8.1.6
\(f_{ hopeMn }\)	Required waste heat ratio for operation judgment standard	-	8.1.6
\(f_{ esub, cgswc }\)	CGS’s auxiliary power ratio (in the presence of a cooling tower)	-	8.1.6
\(f_{ esub, cgsac }\)	CGS’s auxiliary power ratio (in the absence of a cooling tower)	-	8.1.6
\(T_{ AC, c, d }\)	Operation time of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	h/day	8.1.5.2
\(T_{ AC, h, d }\)	Operation time of a heat source group allowing for the use of waste heat of CGS, at date	h/day	8.1.5.2
\(T_{ ST }\)	Maximum operation time of CGS	h/day	8.3
\(T_{ STmin, W }\)	Minimum operation time of CGS when waste heat is used only for hot-water supply	h/day	8.1.6
\(f_{ eope, R }\)	Ratio between power consumption during operation hours and daily power consumption	-	8.8
\(N_{ pri, hr, c }\)	Priority of waste heat use (cooling source)	Number	8.1.5.1
\(N_{ pri, hr, h }\)	Priority of waste heat use (heating source)	Number	8.1.5.1

Table 19. Output
Variable name	Description	Unit	References
\(T_{ cgs, d }\)	Operation time of CGS at date	h/day	8.10
\(f_{ esub, cgs }\)	Power ratio of CGS auxiliary module	-	8.12

A CGS’s auxiliary power ratio, \(f_{ esub, cgs }\), is determined as shown below according to a rated power generation output of the CGS. This ratio is based on that a micro gas engine with a rated power generation output of 50kW or less does not have a cooling tower, and accordingly, its auxiliary power is low.

\[f_{ esub, cgs } = \begin{cases} f_{ esub, cgswc } & , E_{ cgs, rated } > 50 \\ f_{ esub, cgsac } & , E_{ cgs, rated } \leqq 50 \end{cases}\]

An operation time of CGS at a date d, \(T_{ cgs, d }\), is determined form the following formula.

(1) \(n_{ pri, hr, c } = 0 \land n_{ pri, hr, h } = 0 \)

　a) In the case of \(\frac{ q_{ hr, total, d } }{ E_{ cgs, rated } \times 3.6 \times f_{ hopeMn } } \times \frac{ f_{ cgs, e, rated } }{ f_{ cgs, h, rated } } \geqq T_{ ST } \land \frac{ E_{ e, total, d } \times f_{ eope, R } \times ( 1 + f_{ esub, cgs } ) }{ E_{ cgs, rated } \times f_{ eopMn } } \geqq T_{ ST }\)

\[T_{ cgs, d } = T_{ ST }\]

　b) Not falling under (a), \(\left( \frac{ q_{ hr, total, d } }{ E_{ cgs, rated } \times 3.6 \times f_{ hopeMn } } \times \frac{ f_{ cgs, e, rated } }{ f_{ cgs, h, rated } } \geqq T_{ STmin, W } \land \frac{ E_{ e, total, d } \times f_{ eope, R } \times ( 1 + f_{ esub, cgs } ) }{ E_{ cgs, rated } \times f_{ eopMn } } \geqq T_{ STmin, W } \right) = \mbox\{True}\)

\[T_{ cgs, d } = T_{ STmin, W }\]

　c) Not falling under a) or b)

\[T_{ cgs, d } = 0\]

(2) Not falling under (1), \(T_{ AC, c, d } \geqq T_{ AC, h, d }\)

\[T_{ cgs, d } = T_{ ST }\]

　b) Not falling under (a), \frac{ q_{ hr, total, d } }{ E_{ cgs, rated } \times 3.6 \times f_{ hopeMn } } \times \frac{ f_{ cgs, e, rated } }{ f_{ cgs, h, rated } } \geqq T_{ AC, c, d } \land \frac{ E_{ e, total, d } \times f_{ eope, R } \times ( 1 + f_{ esub, cgs } ) }{ E_{ cgs, rated } \times f_{ eopMn } } \geqq T_{ AC, c, d } \right) = \mbox{True}]

\[T_{ cgs, d } = T_{ AC, c, d }\]

　c) Not falling under a) or b)

\[T_{ cgs, d } = 0\]

(3) Not falling under (1), \((T_{ AC, c, d } < T_{ AC, h, d }\)

\[T_{ cgs, d } = T_{ ST }\]

\[T_{ cgs, d } = T_{ AC, h, d }\]

　c) Not falling under a) or b)

\[T_{ cgs, d } = 0\]

(1) is the case where “waste heat is used only for hot-water supply.” In this case, \(T_{ STmin, W }\) (=10 hours) is assumed to a minimum operation time.
2) and (3) are the case in which waste heat is used for cooling or heating. In this case, CGS’s operation time is assumed to be its maximum operation time by reference to the longer of cooling and heating operations if there are sufficient power and heat loads.

\(\frac{ q_{ hr, total, d } }{ E_{ cgs, rated } \times 3.6 \times f_{ hopeMn } } \times \frac{ f_{ cgs, e, rated } }{ f_{ cgs, h, rated } }\) in the conditional expression represents hours of operation time in the case where a heat load of the CGS heat exhaust system is divided by an amount of heat exhaust applicable to the required waste heat ratio for operation judgment standard. Similarly, \(\frac{ E_{ e, total, d } \times f_{ eope, R } \times ( 1 + f_{ esub, cgs } ) }{ E_{ cgs, rated } \times f_{ eopMn } }\) represents hours of operation time in the case where power is generated in the condition applicable to the required power ratio for operation judgment standard. If both of these hours exceed a maximum operation time \(T_{ ST }\), the maximum operation time is assumed to be an operation time of CGS at that day, deeming the sufficiency of the loads, Even in the case where this does not apply, if both of them exceed a cooling or heating operation time (the heating operation time is used if being longer than the cooling operation time), or a “minimum operation time (10 hours) of a CGS in the case where waste heat is used only for hot-water supply,” the relevant time (cooling operation time, heating operation time or minimum operation time) is assumed to be an operation time of the CGS at that day. If they do not meet the above time requirements, the CGS shall not be operated at that day.

(Supplementary document) Detailed manual of formula for conditional expression

8.10 Loads during CGS’s Operation Time

Calculate a load during an operation time of a CGS.

Table 20. Input
Variable name	Description	Unit	Reference
\(E_{ e, total, d }\)	Power consumption of building at date	kWh/day	8.4
\(E_{ AC, ref, c, hr, d }\)	In the use of waste heat, possible amount of reduction of primary energy consumption of a cooling source main module of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	MJ/day	8.6
\(q_{ AC, ref, c, hr, d }\)	Heat exhaust load of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	MJ/day	8.6
\(E_{ AC, ref, h, hr, d }\)	In the use of waste heat, possible amount of reduction of primary energy consumption of a main module of a heat source group allowing for the use of waste heat of CGS, at date	MJ/day	8.1.5.2
\(q_{ AC, ref, h, hr, d }\)	Heat exhaust load of a heat source group allowing for the use of waste heat of CGS, at date	MJ/day	8.1.5.2
\(E_{ W, hr, d }\)	In the use of waste heat, possible amount of reduction of primary energy consumption of a main module of a water heater (system) allowing for the use of waste heat of CGS, at date	MJ/day	8.1.5.2
\(q_{ W, hr, d }\)	Heat exhaust load of a water heater (system) allowing for the use of waste heat of CGS, at date	MJ/day	8.1.5.2
\(T_{ ST }\)	Maximum operation time of CGS	h/day	8.3
\(T_{ AC, c, d }\)	Operation time of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS, at date	h/day	8.1.5.2
\(T_{ AC, h, d }\)	Operation time of a heat source group allowing for the use of waste heat of CGS, at date	h/day	8.1.5.2
\(f_{ eope, R }\)	Ratio between power consumption during operation hours and daily power consumption	-	8.8
\(T_{ cgs, d }\)	Operation time of CGS at date	h/day	8.9

Table 21. Output
Variable name	Description	Unit	References
\(E_{ e, total, on, d }\)	Power consumption of building during CGS operation hours at date	kWh/day	-
\(E_{ AC, ref, c, hr, on, d }\)	In the use of waste heat, possible amount of reduction of primary energy consumption of a cooling source main module of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS during its operation, at date	MJ/day	-
\(q_{ AC, ref, c, hr, on, d }\)	Available waste heat for a cooling source of absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS during its operation, at date	MJ/day	-
\(E_{ AC, ref, h, hr, on, d }\)	Primary energy consumption of a main module of a heat source group allowing for the use of waste heat of CGS during its operation, at date	MJ/day	-
\(q_{ AC, ref, h, hr, on, d }\)	Available waste heat for a heat source group allowing for the use of waste heat of CGS during its operation, at date	MJ/day	-
\(E_{ W, hr, on, d }\)	Primary energy consumption of a water heater (system) allowing for the use of waste heat of CGS, at date	MJ/day	-
\(q_{ AC, ref, h, hr, on, d }\)	Available waste heat for a water heater (system) allowing for the use of waste heat of CGS during its operation, at date	MJ/day	-
\(q_{ total, hr, on, d }\)	Total of available waste heat during CSG operation at date	MJ/day	-

Correct a power consumption of a building during the operation hours of a CGS by its operation time in the following formula.

\[E_{ e, total, on, d } = E_{ e, total, d } \times f_{ eope, R } \times \frac{ T_{ cgs, d } }{ T_{ ST } }\]

Available waste heat for hot-water supply and a primary energy consumption of a water heater (system) allowing for the use of waste heat during the operation hours of the CGS are not corrected by its operation time, based on that loads during non-operation hours of the CGS can be also treated by installing a tank.

\[E_{ W, hr, on, d } = E_{ W, hr, d }\]

\[q_{ W, hr, on, d } = q_{ W, hr, d }\]

During the operation hours of a CGS, available waste heat for a cooling source, and primary energy of a main module is consumed. A possible amount of reduction in the relevant amount and the primary energy consumption is determined from the following formula. If the cooling operation time is shorter than the operation time of a CGS, the relevant energy consumption is not corrected by the operation time of the CGS. If the cooling operation time is longer than the operation time of the CGS, available waste heat for the cooling source during the operation hours of the CGS is determined in proportion to the number of hours.

\[E_{ AC, ref, c, hr, on, d } = \begin{cases} E_{ AC, ref, c, hr, d } & , T_{ AC, c, d } \leqq T_{ cgs, d } \\ E_{ AC, ref, c, hr, d} \times \frac{ T_{ cgs, d } }{ T_{ AC, c, d } } & , T_{ AC, c, d } > T_{ cgs, d } \end{cases}\]

\[q_{ AC, ref, c, hr, on, d } = \begin{cases} q_{ AC, ref, c, hr, d } & , T_{ AC, c, d } \leqq T_{ cgs, d } \\ q_{ AC, ref, c, hr, d} \times \frac{ T_{ cgs, d } }{ T_{ AC, c, d } } & , T_{ AC, c, d } > T_{ cgs, d } \end{cases}\]

Similarly, available waste heat for a heating source , and a primary energy consumption of a main module of a heat source group allowing for the use of waste heat, during the operation hours of the CGS, are determined from the following formula.

\[E_{ AC, ref, h, hr, on, d } = \begin{cases} E_{ AC, ref, h, hr, d } & , T_{ AC, h, d } \leqq T_{ cgs, d } \\ E_{ AC, ref, h, hr, d} \times \frac{ T_{ cgs, d } }{ T_{ AC, h, d } } & , T_{ AC, h, d } > T_{ cgs, d } \end{cases}\]

\[q_{ AC, ref, h, hr, on, d } = \begin{cases} q_{ AC, ref, h, hr, d } & , T_{ AC, h, d } \leqq T_{ cgs, d } \\ q_{ AC, ref, h, hr, d} \times \frac{ T_{ cgs, d } }{ T_{ AC, h, d } } & , T_{ AC, h, d } > T_{ cgs, d } \end{cases}\]

A total of available waste heat amounts during the operation time of a CGS at a date d is determined from the following formula based on the value calculated in the above formula.

\[q_{ total, hr, on, d } = q_{ AC, ref, c, hr, on, d } + q_{ AC, ref, h, hr, on, d } + q_{ W, hr, on, d }\]

8.11 Maximum Number of Operating CGSs

Calculate the maximum number of operating CGSs.

Table 22. Input
Variable name	Description	Unit	Reference
\(q_{ hr, total, d }\)	Heat load of CGS heat exhaust system at date	MJ/day	8.7
\(E_{ cgs, rated }\)	Rated generation output of CGS	kW	8.x
\(f_{ cgs, e, rated }\)	Rated power generation efficiency of CGS (Lower heating value standard)	-	8.1.5.1
\(f_{ cgs, hr, rated }\)	Rated heat exhaust efficiency of CGS (Lower heating value standard)	-	8.1.5.1
\(T_{ cgs, d }\)	Operation time of CGS at date	h/day	8.9
\(N_{ cgs }\)	Number of installed CGSs	Number	8.x

Table 23. Output
Variable name	Description	Unit	References
\(N'_{ cgs, on, max, d }\)	Temporary maximum number of operating CGSs at date	Number	-
\(N_{ cgs, on, max, d }\)	Maximum number of operating CGSs at date	Number	-

The maximum number of operating CGSs at a date d, \(N'_{ cgs, on, max, d }\), is determined form the following formula.

\[N'_{ cgs, on, max, d } = \begin{cases} \left \lceil{ \frac{ q_{ hr, total, d } }{ E_{ cgs,rated } \times 3.6 } \times \frac{ f_{ cgs, e, rated } }{ f_{ cgs, hr, rated } \times T_{ cgs, d } } }\right \rceil & , T_{ cgs, d } \neq 0 \\ 0 & , T_{ cgs, d } = 0 \end{cases}\]

In the case where \(\left \lceil{ x }\right \rceil\) is a function of Ceil and x contains decimals, it is rounded to an integer.

Based on the comparison between the number of installed CGSs and the determined temporary maximum number of operating CGSs, the maximum number of the CGSs is determined.

\[N_{ cgs, on, max, d } = \begin{cases} N_{ cgs } & , N'_{ cgs, on, max, d } \geqq N_{ cgs } \\ N'_{ cgs, on, max, d } & , N'_{ cgs, on, max, d } < N_{ cgs } \end{cases}\]

(Supplementary document) Detailed manual of formula for the temporary maximum number of operating CGSs

8.12 Power Generation Loads

Calculate power generation loads.

Table 24. Input
Variable name	Description	Unit	Reference
\(E_{ e, total, on, d }\)	Power consumption of building during CGS operation hours at date	kWh/day	8.10
\(f_{ esub, cgs }\)	CGS’s auxiliary power ratio	-	8.9
\(f_{ elmax }\)	Maximum share rate of power load of CGS	-	8.1.6

Table 25. Output
Variable name	Description	Unit	References
\(E_{ e, load, d }\)	Power generation load of CGS at date	kWh/day	-

\[E_{ e, load, d} = E_{ e, total, on, d} \times f_{ elmax } \times ( 1 + f_{ esub, cgs } )\]

8.13 Number of Operating CGSs

Calculate the number of operating CGSs.

Table 26. Input
Variable name	Description	Unit	Reference
\(E_{ e, load, d }\)	Power generation load of CGS at date	kWh/day	8.12
\(E_{ cgs, rated }\)	Rated generation output of CGS	kW	8.x
\(N_{ cgs, on, max, d }\)	Maximum number of operating CGSs at date	Number	8.11
\(T_{ cgs, d }\)	Operation time of CGS at date	h/day	8.9

Table 27. Output
Variable name	Description	Unit	References
\(N'_{ cgs, on, d }\)	Temporary value of operating CGSs at date	Number	-
\(N_{ cgs, on, d }\)	Number of operating CGSs at date	Number	-

\[N'_{ cgs, on, d } = \begin{cases} \frac{ E_{ e, load, d } }{ E_{ cgs, rated } \times T_{ cgs, d } } & , T_{ cgs, d } > 0 \\ 0 & , T_{ cgs, d} = 0 \\ \end{cases}\]

\[N_{ cgs, on, d } = \begin{cases} N_{ cgs, on, max, d } & , N'_{ cgs, on, d } \geqq N_{ cgs, on, max, d } \\ \left \lceil{ N'_{ cgs, on, d } }\right \rceil & , N_{ cgs, on, max, d } > N'_{ cgs, on, d } > 0 \\ 0 & , 0 \geqq N'_{ cgs, on, d } \\ \end{cases}\]

In the case where \(\left \lceil{ x }\right \rceil\) is a function of Ceil and x contains decimals, it is rounded to an integer.

8.14 Load Factor of Power Generation

Calculate a load factor of power generation.

Table 28. Input
Variable name	Description	Unit	Reference
\(E_{ e, load, d }\)	Power generation load of CGS at date	kWh/day	8.12
\(E_{ cgs, rated }\)	Rated generation output of CGS	kW	8.1.5.1
\(N_{ cgs, on, d }\)	Number of operating CGSs at date	Number	8.13
\(T_{ cgs, d }\)	Operation time of CGS at date	h/day	8.9

Table 29. Output
Variable name	Description	Unit	References
\(mxL_{ cgs, d }\)	Load factor of CGS at date	-	8.1.15

\[mxL_{ cgs, d } = \begin{cases} \min( 1, \frac{ E_{ e, load, d } }{ E_{ cgs, rated } \times T_{ cgs, d } \times N_{ cgs, on, d } }) & , T_{ cgs, d } > 0 \land N_{ cgs, on, d } > 0 \\ 0 & , T_{ cgs, d} = 0 \lor N_{ cgs, on, d} = 0 \\ \end{cases}\]

8.15 Power Generation and Waste Heat Recovery Efficiencies

Calculate power generation and waste heat recovery efficiencies.

Table 30. Input
Variable name	Description	Unit	Reference
\(f_{ e2 }\)	Coefficient and term of quadratic formula of CGS’s power generation efficiency characteristic expression	-	8.2
\(f_{ e1 }\)	Coefficient and term of linear formula of CGS’s power generation efficiency characteristic expression	-	8.2
\(f_{ e0 }\)	Coefficient and term of CGS’s power generation efficiency characteristic expression	-	8.2
\(f_{ hr2 }\)	Coefficient and term of quadratic formula of CGS’s heat exhaust efficiency characteristic expression	-	8.2
\(f_{ hr1 }\)	Coefficient and term of linear formula of CGS’s heat exhaust efficiency characteristic expression	-	8.2
\(f_{ hr0 }\)	Constant and term of CGS’s heat exhaust efficiency characteristic expression	-	8.2
\(mxL_{ cgs, d }\)	Load factor of CGS at date	-	8.14

Table 31. Output
Variable name	Description	Unit	References
\(mxR_{ e, cgs, d }\)	Power generation efficiency of CGS at date d (Lower heating value standard)	-	8.17
\(mxR_{ hr, cgs, d }\)	Recovery efficiency of waste heat from CGS at date d (Lower heating value standard)	-	8.17

Determine a power generation efficiency (lower heating value standard) of a model group I, \(mxR_{ e, cgs, d }\), and a waste heat recovery efficiency of the group (lower heating value standard), at a date d, from the following formula.

\[mxR_{ e, cgs, d } = f_{ e2 } \times mxL_{ cgs, d }^2 + f_{ e1 } \times mxL_{ cgs, d } + f_{ e0 }\]

\[mxR_{ hr, cgs, d } = f_{ jr2 } \times mxL_{ cgs, d }^2 + f_{ hr1 } \times mxL_{ cgs, d } + f_{ hr0 }\]

8.16 Power Generation and Effective Power Generation

Calculate a power generation and effective power generation.

Table 32. Input
Variable name	Description	Unit	Reference
\(E_{ cgs, rated }\)	Rated power generation of CSG at date	kW	8.1.5
\(N_{ cgs, on, d }\)	Number of operating CGSs at date	Number	8.13
\(T_{ cgs, d }\)	Operation time of CGS at date	h/day	8.11
\(mxL_{ cgs, d }\)	Load factor of CGS at date	-	8.14
\(f_{ esub, cgs }\)	CGS’s auxiliary power ratio	-	8.9

Table 33. Output
Variable name	Description	Unit	References
\(E_{ e, cgs, d }\)	Power generation of CGS at date	kWh/day	-
\(E_{ ee, cgs, d }\)	Effective power generation of CGS at date	kWh/day	-

\[E_{ e, cgs, d } = E_{ cgs, rated } \times N_{ cgs, on, d } \times T_{ cgs, d } \times mxL_{ cgs, d }\]

\[E_{ ee, cgs, d } = \frac{ E_{ e, cgs, d } }{ 1 + f_{ esub, cgs } }\]

8.17 Fuel Consumption and Waste Heat Recovery

Calculate a fuel consumption and waste heat recovery.

Table 34. Input
Variable name	Description	Unit	Reference
\(E_{ e, cgs, d }\)	Power generation of CGS at date	kWh/day	8.16
\(mxR_{ e, cgs, d }\)	Power generation efficiency of CGS at date d (Lower heating value standard)	-	8.15
\(mxR_{ hr, cgs, d }\)	Waste efficiency of heat recovery from CGS at date d (Lower heating value standard)	-	8.15
\(f_{ lh }\)	Ratio of lower to higher heating value of gas	-	8.1.6
\(f_{ cgs, e, cor }\)	Correction of generation efficiency	-	8.1.6

Table 35. Output
Variable name	Description	Unit	References
\(E_{ s, cgs, d }\)	Fuel consumption of CGS at date d (Higher heating value standard)	MJ/day	8.22
\(q_{ hr, cgs, d }\)	Waste heat recovery from CGS at date	MJ/day	8.18

\[E_{ s, cgs, d } = \begin{cases} 0 & , E_{ e, cgs, d } = 0 \\ E_{ e, cgs, d } \times \frac{ 3.6 }{ mxR_{ e, cgs, d } \times f_{ cgs, e, cor } \times f_{ lh } } &, E_{ e, cgs, d } \neq 0 \end{cases}\]

\[q_{ hr, cgs, d } = E_{ s, cgs, d } \times f_{ cgs, e ,cor } \times mxR_{ hr, cgs, d } \times f_{ lh }\]

The fuel consumption of a CGS is multiplied by a power generation efficiency correction in the formula for waste heat recovery from the GCG, \(q_{ hr, cgs, d }\), because the effect given when the fuel consumption of the CGS (Higher heating value standard) \(E_{ s, cgs, d }\) is multiplied by \(f_{ cgs, e, cor }\) as a power generation efficiency correction value is cancelled out. This is due to that the power generation efficiency correction \(f_{ cgs, e, cor }\) is intended to increase the fuel consumption and not intended for resultant increase of the waste heat recovery.

8.18 Effective Waste Heat Recovery

Calculate an effective waste heat recovery.

Table 36. Input
Variable name	Description	Unit	Reference
\(q_{ hr, cgs, d }\)	Waste heat recovery from CGS at date	MJ/day	8.17
\(q_{ total, hr, on, d }\)	Total of available waste heat amounts during CGS operation at date	MJ/day	8.10
\(f_{ hr, loss }\)	Heat loss rate of waste heat	-	8.1.6

Table 37. Output
Variable name	Description	Unit	References
\(q_{ ehr, cgs, d }\)	Effective waste heat recovery at date	MJ/day	8.19

\[q_{ hr, cgs, d } = \begin{cases} q_{ total, hr, on, d } & , q_{ hr, cgs, d } \times f_{ hr, loss } \geqq q_{ total, hr, on, d} \\ q_{ hr, cgs, d } \times f_{ hr, loss } & , q_{ hr, cgs, d } \times f_{ hr, loss } < q_{ total, hr, on, d } \end{cases}\]

8.19 Waste Heat Usage in Each Use

Calculate a waste heat usage in each use.

Table 38. Input
Variable name	Description	Unit	Reference
\(q_{ ehr, cgs, d }\)	Effective waste heat recovery amount at date	MJ/day	8.18
\(q_{ AC, ref, c, hr, on, d }\)	Available waste heat for cooling source of absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS during its operation, at date	MJ/day	8.10
\(q_{ AC, ref, h, hr, on, d }\)	Available waste heat for heat source group allowing for the use of waste heat during CGS operation time, at date	MJ/day	8.10
\(q_{ W, hr, on, d }\)	Available waste heat for water heater (system) allowing for the use of waste heat during CGS operation time, at date	MJ/day	8.10
\(n_{ pri, hr, c }\)	Priority of waste heat use (cooling source)	-	8.1.5.2
\(n_{ pri, hr, h }\)	Priority of waste heat use (heating source)	-	8.1.5.2
\(n_{ pri, hr, W }\)	Priority of waste heat use (hot-water supply)	-	8.1.5.2

Table 39. Output
Variable name	Description	Unit	References
\(q_{ AC, ref, c, ehr, d }\)	Waste heat usage for a cooling source of an absorption chiller/heater with auxiliary waste heat system recovery (system), at date	MJ/day	8.20
\(q_{ AC, ref, h, ehr, d }\)	Waste heat usage of heat source group at date	MJ/day	8.20
\(q_{ W, ehr, d }\)	Waste heat usage of water heater (system) at date	MJ/day	8.20
\(q_{ pri1, ehr, d }\)	Waste heat usage in use with priority order 1st at date	MJ/day	-
\(q_{ pri2, ehr, d }\)	Waste heat usage in use with priority order 2nd at date	MJ/day	-
\(q_{ pri3, ehr, d }\)	Waste heat usage in use with priority order 3rd at date	MJ/day	-
\(q_{ pri1, ehr, on, d }\)	Available waste heat in use with the priority order 1st at date	MJ/day	-
\(q_{ pri2, ehr, on, d }\)	Available waste heat in use with the priority order 2nd at date	MJ/day	-
\(q_{ pri3, ehr, on, d }\)	Available waste heat in use with the priority order 3rd at date	MJ/day	-

Calculate a waste heat usage in each use at a date d according to the priority order of use of waste heat.

First, allocate an available waste heat to the use with the priority order 1st (one of cooling, heating or hot-waster supply) to \(q_{pri1,ehr,on,d}\), and also that with the priority order 2nd and 3rd according to the priority order of use of waste heat.

\[q_{ pri1, ehr, on, d } = \begin{cases} q_{ AC, ref, c, hr, on ,d } & , n_{ pri, hr, c } = 1 \\ q_{ AC, ref, h, hr, on ,d } & , n_{ pri, hr, h } = 1 \\ q_{ W, hr, on ,d } & , n_{ pri, hr, W } = 1 \end{cases}\]

\[q_{ pri2, ehr, on, d } = \begin{cases} q_{ AC, ref, c, hr, on ,d } & , n_{ pri, hr, c } = 2 \\ q_{ AC, ref, h, hr, on ,d } & , n_{ pri, hr, h } = 2 \\ q_{ W, hr, on ,d } & , n_{ pri, hr, W } = 2 \\ 0 & , \mbox{Others} \end{cases}\]

\[q_{ pri3, ehr, on, d } = \begin{cases} q_{ AC, ref, c, hr, on ,d } & , n_{ pri, hr, c } = 3 \\ q_{ AC, ref, h, hr, on ,d } & , n_{ pri, hr, h } = 3 \\ q_{ W, hr, on ,d } & , n_{ pri, hr, W } = 3 \\ 0 & , \mbox{Others} \end{cases}\]

Next, if an effective waste heat recovery obtained from a CGS, \(q_{ ehr, cgs, d }\), is larger than an available waste heat with the priority order 1st, \(q_{ pri1, ehr, on, d }\) (in the case of the following (1)), calculate how much hot water is available to the use with the priority order 2nd, on the assumption that all of the available waste heat with the priority order 1st, \(q_{ pri1, ehr, on, d }\) can be supplied. In the same way, calculate it for the use with the priority order 3rd.

(1) In the case of \(q_{ ehr, cgs, d } \geqq q_{ pri1, ehr, on, d } \)

\[q_{ pri1, ehr, d } = q_{ pri1, ehr, on, d }\]

　a) In the case of \(q_{ ehr, cgs, d } - q_{pri1, ehr, d } \geqq q_{ pri2, ehr, on, d }\)

\[q_{ pri2, ehr, d } = q_{ pri2, ehr, on, d }\]

　　i) In the case of \(q_{ehr, cgs, d } - q_{ pri1, ehr, d } - q_{ pri2, ehr, d } \geqq q_{ pri3, ehr, on, d }\)

\[q_{ pri3, ehr, d } = q_{ pri3, ehr, on, d }\]

　　ii) In the case of \(q_{ehr, cgs, d } - q_{ pri1, ehr, d } - q_{ pri2, ehr, d } < q_{ pri3, ehr, on, d }\)

\[q_{ pri3, ehr, d } = q_{ ehr, cdg, d } - q_{ pri1, ehr, d } - q_{ pri2, ehr, d }\]

　ii) In the case of \(q_{ ehr, cgs, d } - q_{pri1, ehr, d } < q_{ pri2, ehr, on, d }\)

\[q_{ pri2, ehr, d } = q_{ ehr, cgs, d } - q_{ pri1, ehr, d }\]

\[q_{ pri3, ehr, d } = 0\]

(2) In the case of \(q_{ ehr, cgs, d } < q_{ pri1, ehr, on, d } \)

\[q_{ pri1, ehr, d } = q_{ ehr, cgs, d }\]

\[q_{ pri2, ehr, d } = 0\]

\[q_{ pri3, ehr, d } = 0\]

Finally, after determining how much waste heat is available to the uses with the priority orders 1st. 2nd and 3rd in the above (1) or (2), allocate determined available waste heat to cooling, heating and hot-water supply.

\[q_{ AC, ref, c, ehr, d } = \begin{cases} 0 & , n_{ pri, hr, c } = \mbox{blank} \\ q_{ pri1, ehr, d } & , n_{ pri, hr, c } = 1 \\ q_{ pri2, ehr, d } & , n_{ pri, hr, c } = 2 \\ q_{ pri3, ehr, d } & , n_{ pri, hr, c } = 3 \end{cases}\]

\[q_{ AC, ref, h, ehr, d } = \begin{cases} 0 & , n_{ pri, hr, h } = \mbox{blank} \\ q_{ pri1, ehr, d } & , n_{ pri, hr, h } = 1 \\ q_{ pri2, ehr, d } & , n_{ pri, hr, h } = 2 \\ q_{ pri3, ehr, d } & , n_{ pri, hr, h } = 3 \end{cases}\]

\[q_{ W, ehr, d } = \begin{cases} 0 & , n_{ pri, hr, W } = \mbox{blank} \\ q_{ pri1, ehr, d } & , n_{ pri, hr, W } = 1 \\ q_{ pri2, ehr, d } & , n_{ pri, hr, W } = 2 \\ q_{ pri3, ehr, d } & , n_{ pri, hr, W } = 3 \end{cases}\]

8.20 Reduction of Primary Energy in Each Use

Calculate a reduction of primary energy in each use.

Table 40. Input
Variable name	Description	Unit	Reference
\(E_{ AC, ref, c, hr,on, d }\)	In the use of waste heat, possible amounts of reduction in primary energy consumption of a cooling source main module of an absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS during its operation, at date	MJ/day	8.10
\(E_{ AC, ref, h, hr,on, d }\)	Primary energy consumption of a main module of a heat source group allowing for the use of waste heat of CGS during its operation, at date	MJ/day	8.10
\(E_{ W, hr,on, d }\)	Primary energy consumption of a water heater (system) allowing for the use of waste heat of CGS, at date	MJ/day	8.10
\(q_{ AC, ref, c, hr, on, d }\)	Available waste heat for cooling source of absorption chiller/heater with auxiliary waste heat system recovery (system) allowing for the use of waste heat of CGS during its operation, at date	MJ/day	8.10
\(q_{ AC, ref, h, hr, on, d }\)	Available waste heat for heat source group allowing for the use of waste heat during CGS operation time, at date	MJ/day	8.10
\(q_{ W, hr, on, d }\)	Available waste heat for water heater (system) allowing for the use of waste heat during CGS operation time, at date	MJ/day	8.10
\(q_{ AC, ref, c, ehr, d }\)	Waste heat usage for a cooling source of an absorption chiller/heater with auxiliary waste heat system recovery (system), at date	MJ/day	8.19
\(q_{ AC, ref, h, ehr, d }\)	Waste heat usage of heat source group at date	MJ/day	8.19
\(q_{ W, hr, on, d }\)	Waste heat usage of water heater (system) at date	MJ/day	8.19

Table 41. Output
Variable name	Description	Unit	References
\(E_{ AC, ref, c, red, d }\)	Reduction of primary energy of cooling at date	MJ/day	8.22
\(E_{ AC, ref, h, red, d }\)	Reduction of primary energy of heating at date	MJ/day	8.22
\(E_{ W, red, d }\)	Reduction of primary energy of hot-water supply at date	MJ/day	8.22

A reduction of primary energy of cooling at a date d, \(E_{ AC, ref, c, red, d }\), is determined from the following formula.

\[E_{ AC, ref, c, red, d } = \begin{cases} 0 & , q_{ AC, ref, c, hr, on, d } = 0 \\ E_{ AC, ref, c, hr, on ,d } \times \frac{ q_{ AC, ref, c, ehr, d } }{ q_{ AC, ref, c, hr, on, d } } & , \mbox{Others} \end{cases}\]

A reduction of primary energy of heating at a date d, \(E_{ AC, ref, h, red, d }\), is determined from the following formula.

\[E_{ AC, ref, h, red, d } = \begin{cases} 0 & , q_{ AC, ref, h, hr, on, d } = 0 \\ E_{ AC, ref, h, hr, on ,d } \times \frac{ q_{ AC, ref, h, ehr, d } }{ q_{ AC, ref, h, hr, on, d } } & , \mbox{Others} \end{cases}\]

A reduction of primary energy of heating at a date d, \(E_{ W, red, d }\), is determined from the following formula.

\[E_{ W, red, d } = \begin{cases} 0 & , q_{ W, hr, on, d } = 0 \\ E_{ W, hr, on ,d } \times \frac{ q_{ W, ehr, d } }{ q_{ W, hr, on, d } } & , \mbox{Others} \end{cases}\]

These formulas are based on the concept that a primary energy consumption of waste heat utilization equipment (a heater, an air conditioner or a water heater) is reduced according to a ratio between available waste heat and actually used waste heat.

8.21 Reduction of Primary Energy of Electric Power

Calculate a reduction of primary energy of electric power.

Table 42. Input
Variable name	Description	Unit	Reference
\(E_{ ee, cgs, d }\)	Effective power generation of CGS at date	kWh/day	8.16

Table 43. Output
Variable name	Description	Unit	References
\(E_{ e, red, d }\)	Reduction of primary energy of power generation at date	MJ/day	8.22

\[E_{ e, red, d } = E_{ ee, cgs, d } \times f_{ prim, e }\]

8.22 Reduction of Primary Energy of CGS

Calculate a reduction of primary energy of a CGS.

Table 44. Input
Variable name	Description	Unit	Reference
\(E_{ s, cgs }\)	Fuel consumption of CGS at date d (Higher heating value standard)	MJ/day	8.17
\(E_{ AC, ref, c, red, d }\)	Reduction of primary energy of cooling at date	MJ/day	8.20
\(E_{ AC, ref, h, red, d }\)	Reduction of primary energy of heating at date	MJ/day	8.20
\(E_{ W, red, d }\)	Reduction of primary energy of hot-water supply at date	MJ/day	8.20
\(E_{ AC, ref, c, red, d }\)	Reduction of primary energy of cooling at date	MJ/day	8.20
\(E_{ e, red, d }\)	Reduction of primary energy of power generation at date	MJ/day	8.21

Table 45. Output
Variable name	Description	Unit	References
\(E_{ total, cgs, red, d }\)	Reduction of primary energy of CGS at date	MJ/day	Output

\[E_{ total, cgs, red, d } = E_{ AC, ref, c, red, d } + E_{ AC, ref, h, red, d } + E_{ W, red, d } + E_{ e, red, d } - E_{ s, cgs, d }\]

Annex G (Cogeneration System)

G.1 Correction of generation efficiency

Table 46. Constant
Constant name	Description	Unit	Value
\(f_{ cgs, e, cor }\)	Correction of generation efficiency	-	0.99

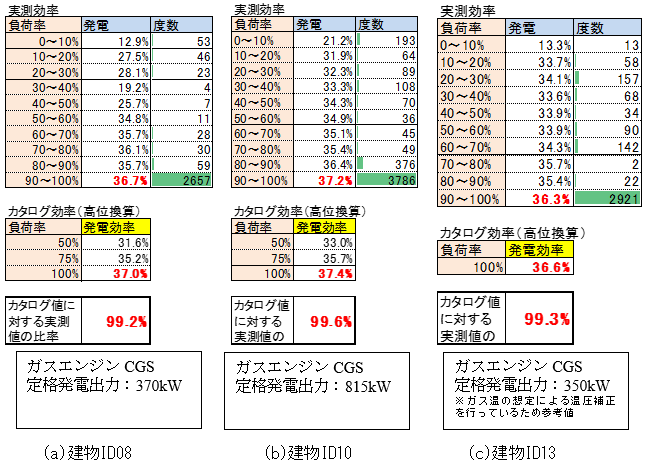
From 3 actual measurement data from the previous survey[3], a comparison between actual power generation efficiencies and catalog values (based on the performance test method that is prescribed in JIB 8122) was made, and as a result, Figure 4 was obtained. Based on this table, \(f_{ cgs, e, cor } = 0.99\) was set as a correction of power generation efficiency.

Figure 4. Distribution of actual power generation efficiencies

G.2 Heat loss rate of waste heat

Table 47. Constant
Constant name	Description	Unit	Value
\(f_{ hr, loss }\)	Heat loss rate of waste heat	-	0.97

Waste heat from a CGS is lost from the surface of its pipe during its operation, and the heat is lost because the temperature of circulating water in the pipe is lowered due to its intermittent operation. These losses of the heat were calculated based on the piping specifications of discharging hot water circuits that were obtained from two actual buildings.

The assumed piping specifications are shown in Table 48. The result of calculating the losses of waste heat from the surfaces of the pipes in the discharging hot water circuits of the two buildings based on the specifications shown in Table 48 is shown in Table 49. Where, the temperature of the circulating water is assumed to be 85℃, and the ambient temperatures of the pipes to be 15℃. Next, the result of calculating the heat loss caused by lowering of the in-pipe circulating water is shown in Table 50. On the assumption that the temperature of the circulating water is reduced from 85℃ to 15℃ after a CGS stops, waste heat that is lost due to the lowering of the temperature was assumed to be unavailable waste heat. Based on the unavailable waste heat, the losses of waste heat from the pipes were totalized and compared with the rated heat exhaust of the CGS. The comparison between the two is shown in Table 51. In this case, the operation time of the CGS was assumed to be 12 hours. As a result, the heat losses of 2.7% and 1.7% in Buildings A and B were expected, respectively. Accordingly, about 3% of obtained waste heat was considered to be lost, and a coefficient of the heat loss was set as \(f_{ hr, loss } = 0.97\).

Table 48. Piping specifications
Building	Total of rated heat exhausts of CGS	Pipe length (pipe diameter)
Building A	38.4kW × 1	47.8m（25A） + 5.2m（32A）
Building B	52.5kW × 4	14.0m（50A） + 11.0m（80A） + 27.0m（100A）

Table 49. Heat loss from the surface of pipe during operation of CGS
Building	Pipe length	Pipe diameter	Assumed insulation thickness [bib._G-2]	Insulation specifications [5]	Linear heat loss coefficient	Temperature difference	Heat loss	Total of heat losses
-	m	A	mm	-	W/(m・K)	K	W	W
Building A	47.8	25	20	Insulation specifications 2	0.270	70	903	1032
Building A	5.2	32	20	Insulation specifications 2	0.354	70	129	1032
Building B	14.0	50	20	Insulation specifications 3	0.388	70	380	2089
	11.0	80	20	Insulation specifications 3	0.388	70	478
	27.0	100	25	Insulation specifications 2	0.651	70	1230

Table 50. Heat loss due to intermittent operation
Building	Pipe length	Pipe diameter	Amount of holding water	Temperature difference	Heat loss amount	Total of heat loss amounts
-	m	A	m³	K	Wh	Wh
Building A	47.8	25	0.0023	70	1904	2243
Building A	5.2	32	0.0040	70	339	2243
Building B	14.0	50	0.0270	70	2231	23928
	11.0	80	0.0550	70	4487
	27.0	100	0.0080	70	17210

Table 51. Ratio of heat loss to rated waste heat recovery amounts
Building	Surface heat loss	Assumed operation time	Surface heat loss amount	Heat loss amount due to intermittent operation	Total of heat loss amounts	Accumulated daily waste heat amount	Heat loss ratio
-	W	Hours	kWh	kWh	kWh	kWh	%
Building A	1032	12	12.4	2.2	14.6	537.6	2.7
Building B	2089	12	25.1	23.9	49.0	2940.0	1.7

G.3 CGS auxiliary module power ratio

Table 52. Constant
Constant name	Description	Unit	Value
\(f_{ esub, cgswc }\)	CGS’s auxiliary power ratio (in the presence of a cooling tower)	-	0.05
\(f_{ esub, cgsac }\)	CGS’s auxiliary power ratio (in the absence of a cooling tower)	-	0.06

From one actual measurement datum from the previous survey[3], main module powers and power generation outputs during operation were averaged, and as a result, Table 53 was obtained. In CASCADEⅢ [bib._G-4] used as reference for this program, an auxiliary power of a CGS is expected to be 5% of its power generation output, but actually was close to 6% of the output. In particular, the auxiliary powers of a cooling tower and and pump accounts for 1% of the output. In a large CGS with a cooling tower for heat dissipation, its auxiliary power is assumed to be larger, so in the case where a micro CGS (power generation output of 50kW or less) does not require a cooling tower because it has a radiator for heat dissipation, its auxiliary power ratio was traditionally set as \(f_{ esub, cgsac } = 0.05\), while an auxiliary power ratio of a larger CGS was set as \(f_{ esub, cgswc } = 0.06\).

Table 53. Ratio of CSG’s auxiliary power to its power generation
Building ID01 Gas engine CGS Rated power generation output: 700kW		CGS’s power generation output	Auxiliary power
		CGS’s power generation output	CGS body	Hot water circulating pump	Cooling tower fan	Cooling tower pump	Total
Winter season	Electric power	700W	17.4W	11.1W	0.4W	3.3W	32.2W
Winter season	Power generation output ratio	-	2.5%	1.6%	0.1%	0.5%	4.6%
Intermediate season	Electric power	700W	22.4W	11.1W	2.9W	3.4W	39.8W
Intermediate season	Power generation output ratio	-	3.2%	1.6%	0.4%	0.5%	5.7%
Summer season	Electric power	700W	22.6W	11.0W	4.2W	3.3W	41.1W
Summer season	Power generation output ratio	-	3.2%	1.6%	0.6%	0.5%	5.9%

G.4 Maximum operation time of CGS in the case of intermittent operation.

Table 54. Constant
Constant name	Description	Unit	Value
\(T_{ STn }\)	Maximum operation time of CGS in the case of intermittent operation.	h/day	14

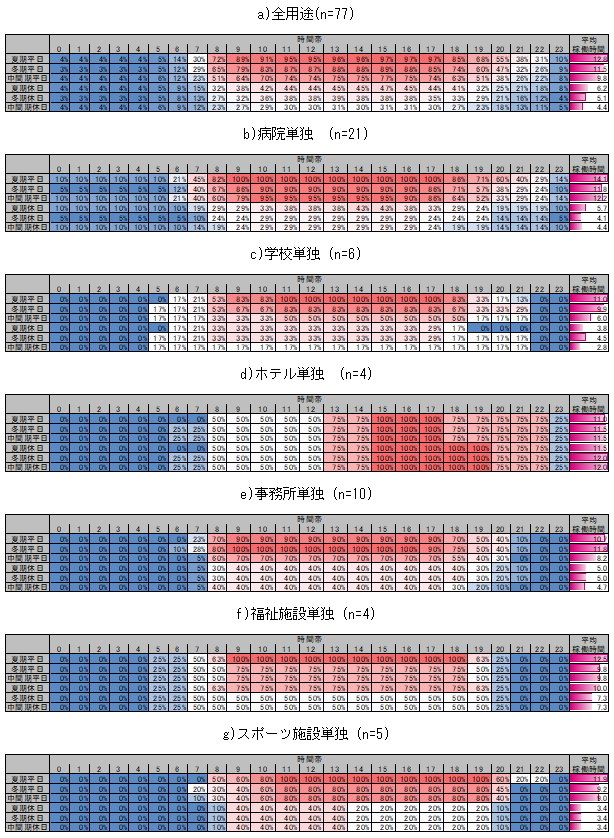
77 buildings with the introduction of a CGS responded to the questionnaire investigation of the previous survey[3]. The hourly availabilities of the CGS in these buildings were analyzed, and as a result, Table 55 was obtained. Table 55 shows the averaged hourly availability of the CGS in all uses and the total of its hourly availabilities in major uses. The availability of the CGS slightly depends on building uses, but the availability is high during 8:00 and 19:00 in a weekday of a summer season. In a hospital with the longest operation time of the CGS, the average operation time of the CGS in the weekday of during a summer season is about 14 hours. A trend in operation hours of the CGS in a hotel is greatly different from those in other uses, but the operation time of the GGS in the hotel is about 11 hours. The relevant operation time in the hotel is not so different from those in other uses.

The hearing survey for system designers that was separately conducted indicates the design concept that estimated hours based on the durable operation hours of the CGS (about 60000 hours but depending on each type of equipment) are 3000 to 4000, assuming that the durable period of the CGS is 15 years to 20 years. From the results of the questionnaire investigation and the hearing survey, assuming that the CGS does not operate on days with small loads such as holidays and days during the intermediate season, and judging that it is reasonable to assume that its maximum operation time per day is approximately 14 hours, the relevant time was set as \(T_{ STn } = 14\), regardless of building uses.

Hours availabilities of CGU in all building uses

G.5 COP of absorption chiller/heater with auxiliary waste heat system recovery at use of waste heat

Table 56. Constant
Constant name	Description	Unit	Value
\(f_{ COP, link, hr }\)	COP at use of waste heat from absorption chiller/heater with auxiliary waste heat recovery	-	0.75

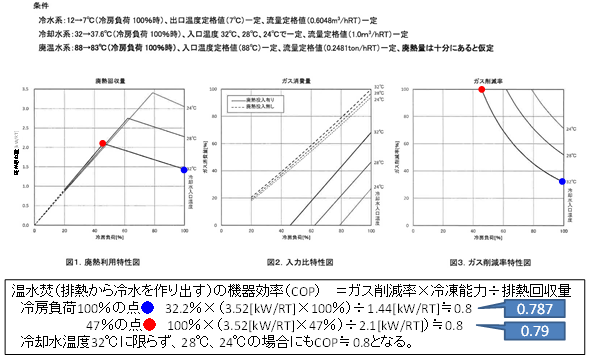
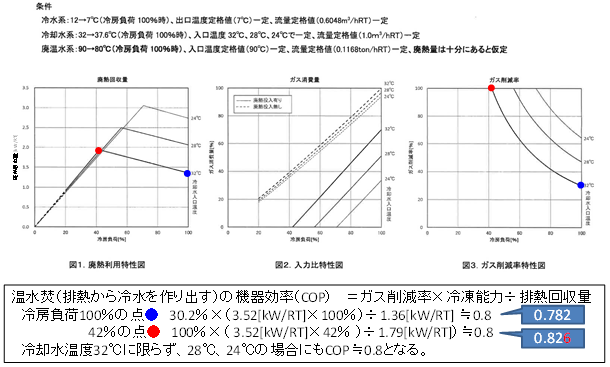
A manufacturer of absorption chillers/heaters with auxiliary waste heat system recovery provided data on the available waste heat amounts and gas consumptions of two models (Figure 5 and Figure 6). Based on the data, a COP (Coefficient Of Performance) the chiller/heater of the in the case where only waste heat is used to manufacture a cooling source was calculated and determined to be approximately 0.79 to 0.82. Accordingly, the relevant coefficient was set as \(f_{ COP, link, hr } = 0.75\).

Figure 5. Characteristic of available waste heat (Equipment A)

Figure 6. Characteristic of available waste heat (Equipment B)

G6. Required power ratio for operation judgment standard.and required heat ratio for operation judgment standard.

Table 57. Constant
Constant name	Description	Unit	Value
\(f_{ eopeMn }\)	Required power ratio for operation judgment standard	-	0.5
\(f_{ hopeMn }\)	Required waste heat ratio for operation judgment standard	-	0.5

A required power ratio for operation judgment standard indicates how much power load is required to operate a CGS in comparison with a required heat ratio for operation judgment standard. The required heat ratio for operation judgment standard also indicates how much heat load is required to operate a CGS in comparison with a rated waste heat recovery. A judgment on whether to operate the CGS when the heat load is small depends on different buildings, and is often left up to site operation managers in the buildings For this reason, it is difficult to set a uniform load value that can be applied to every building, but a load factor of 50% is described in the performance test method for CGSs that is prescribed in JIB 8122. Some buildings where even in actual operation of the CGS, the CGS is operated at a partial load factor of about 50%, are observed. Accordingly, these ratios were set as \(f_{ eopeMn } = 0.5\) and \(f_{ eopeMn } = 0.5\).

G.7 Maximum share ratio of power load of CGS

Table 58. Constant
Constant name	Description	Unit	Value
\(f_{ elmax }\)	Maximum share rate of power load of CGS	-	0.95

Currently, power load control to cover all of power loads with generation of a CGS is not made. The common way of operating the CGS is to introduce power load control under which a part of electric power is always purchased to avoid a reverse power flow from occurring. In CASCADEⅢ [bib._G-4], a default setting is to ensure 5% of an annual peak power as power to be purchased. In reference to this default setting, assuming that at least 5% of the power load is covered by purchasing electric power, the maximum share ratio was set as \(f_{ elmax } = 0.95\).

G.8 Available waste heat (rated condition) during rated operation of absorption chiller/heater with auxiliary waste heat system recovery and maximum load factor (rated condition) at possible operation of the chiller/heater with the use of only waste heat

Table 59. Constant
Constant name	Description	Unit	Value
\(f_{ link, rated, b }\)	Availability rate of waste heat of absorption chiller/heater with auxiliary waste heat system recovery during its rated operation	-	0.15
\(f_{ link, min, b }\)	Maximum loading factor at which a waste heat of absorption chiller/heater with auxiliary waste heat system recovery can operate only by waste heat	-	0.3

The default values in CASCADEⅢ [bib._G-4] were employed for these values.

G9. Rate of reduction of available waste heat by waste heat temperature

Table 60. Constant
Constant name	Description	Unit	Value
\(f_{ link, down }\)	Rate of reduction of available waste heat by waste heat temperature	-	0.125

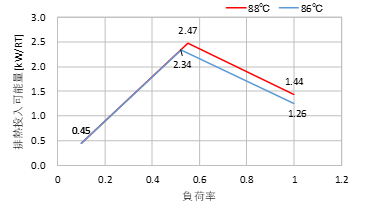
2 measured values in the previous survey [3] show a distribution of inlet temperatures of hot water that is discharged from an absorption chiller/heater with auxiliary waste heat system recovery, indicated in Figure 7. The two measured values show that the actual inlet temperatures of the absorption chillers/heaters with auxiliary waste heat system recovery are lower than their rated inlet temperature. In Building ID04, a first absorption chiller/heater with auxiliary waste heat system recovery is continuously connected to a second one, and discharged hot water after hot water is used in the first unit is charged into the second one. This is also considered to cause the inlet temperature of discharged hot water to be lower than the rated value of the equipment. Based on these results, the inlet temperature of hot water discharged from the absorption chiller/heater with auxiliary waste heat system recovery was considered to become approximately 2℃ lower that its rated value. Therefore, the characteristics of absorption chillers/heaters with auxiliary waste heat system recovery of two manufacturers were examined concerning their available waste heat amounts in the case where the temperatures of the discharged hot water in the chillers/heaters are reduced by 2℃. The characteristic of the equipment that was more affected by the reduction of the temperature is shown in Figure 8. As shown in the figure, when the temperature of the discharged hot water is reduced by 2℃, the available waste heat is reduced by 12.5% at a load factor of 1.0. Accordingly, the relevant reduction rate was set as \(f_{ link, down } = 0.125\).

Figure 7. Distribution of discharged hot water inlet temperatures of absorption chiller/heater with auxiliary waste heat system recovery

Figure 8. Characteristic of available waste heat for absorption chiller/heater with auxiliary waste heat system recovery

G.10 Read of calculation results of other systems/ installations

G.10.1 Total of daily power consumptions (conversion to primary energy)

For the items of air conditioning equipment, mechanical ventilation equipment, lighting installations, hot-water supply systems. elevators, systems with effective use of energy (solar power system) and other, their total daily power consumptions are outputted as described below. These daily power consumptions are required to calculate a power load of a cogeneration system.

Air conditioning equipment \(E_{ AC, total, d }\)

Output the following 4 total daily values [MWh/d].
1. Power consumption of air conditioner group （MWh）\(E_{AC, ahu, i}\)
2. Power consumption of secondary pump group (MWh) \(E_{ AC, pump, i }\)
3. Power consumption of main module of heat source group (MWh) \(E_{ AC, ref, i }\)
4. Power consumption of main module of heat source group (MWh) \(E_{ AC, ref, sub, i }\)
However, note the following requirements.
- The primary energy consumption of a main module of a heat source group, \(E_{AC, ref, i }\) (Formula 2.1.98/ [5] p191) shall be accumulated for only heat source equipment using electric power as an energy source, while that of heat source equipment using other energy sources shall not be accumulated.
- The power consumption of a main module of a heat source system group that is designated in Form 7-3 “⑪ Name of air conditioning heat source group (heating source) using waste heat” is not accumulated.
  
  This is due to that the primary energy consumption of the main module of the heat source system that uses waste heat is reduced when a heat source load is covered by the waste heat, and so, the power load is overestimated if this consumption is estimated as a cogeneration power load.
Mechanical ventilation equipment \(E_{ V, total, d }\)

The power consumption of mechanical ventilation equipment (MWh) \(E_{ v }\) (Formula 2.2.1/ [5] p283) is divided into each daily unit. The primary energy consumption that is equivalent to the total of daily consumption values is outputted.
- In the case where the equipment whose operation schedule is specified for a weekday or holidays, the power consumption is divided into each daily unit according to the relevant schedule. In the case where mechanical ventilation equipment whose annual operation hours is specified, the accumulated consumption value is divided by its operation days in a year. The result is a value of a one-day consumption.
Lighting installation \(E_{ L, total, d }\)

The power consumption of a lighting installation (MWh) \(E_{ L }\) (Formula 2.3.1/[5] p295) is divided into each daily unit. The primary energy consumption that is equivalent to the total of daily consumption values is outputted.
- In the case where the equipment whose operation schedule is specified for a weekday or holidays, the power consumption is divided into each daily unit according to the relevant schedule. In the case where mechanical ventilation equipment whose annual operation hours is specified, the accumulated consumption value is divided by its operation days in a year. The result is a value of a one-day consumption.
Hot-water supply system \(E_{ W, total, d }\)

The accumulated value of the power consumption of a hot-water supply system (targeted to only water heaters using electric power as an energy source)(MWh) \(E_{ w }\) (Formula 2.4.1/[5] p306) is divided into each daily unit. The primary energy consumption that is equivalent to the total of daily consumption values is outputted.
- When being divided into each daily unit, the energy consumption in a room with 365 annual days of hot-water supply is divided by 365. In the case where the annual days of hot-water supply is consistent with those under a room use pattern 1 in other room, the annual primary energy consumption of the hot-water supply system is divided by the annual days. The result is equivalent to a daily energy consumption under the room use pattern 1. Otherwise, an energy consumption obtained after an annual energy consumption of the hot-water supply system is divided by annual days of hot-water supply is equal to a daily energy consumption under the room use patterns 1 and 2.
- In the case where a fuel type of a water heater that is designated in Form 7-3 “⑫ Name of water heater using waste heat” is electric power, the primary energy consumption of this equipment is not accumulated.
  
  This is due to that the primary energy consumption of a water heater in a system using waste heat is reduced when a hot-water supply load is covered by the waste heat, and so, the power load is overestimated if this consumption is estimated as a cogeneration power load.
Elevator \(E_{ EV, total, d }\)

The power consumption of an elevator (MWh) \(E_\{EV}\) (Formula 2.5.1/[5] p314) is divided into each daily unit. The primary energy consumption that is equivalent to the total of daily consumption values is outputted.
- When being divided into each daily unit, the daily power consumption is determined as calculated based on the annual operation hours of the elevator \(T_{ EV, i }\)([5] p316). The annual lighting hours under the standard use conditions in an elevator’s room use as “a room mainly providing service” are equal to the operation hours. That is to say, the power consumption of the elevator is divided into a daily unit in the same way when the primary energy for lighting is divided into a daily unit in the “room mainly providing service.”
Systems with effective use of energy (solar power generation) \(E_{ PV, total, d }\)

The accumulated daily value of a solar power system’s self-consumption of its generation \(E_{ PV_consumption }\)(Formula 2.6.5・Formula 2.6.6/ [5] p327) is outputted.
Other \(E_{ M, total, d }\)

Other power consumption (MWh) \(E_\{M}\) (Formula 3.6.1/[5] p402) is divided into each daily unit. The primary energy consumption that is equivalent to the total of daily consumption values is outputted. The power consumption is divided into each daily unit according to equipment’s heating schedule for each room use.

G.10.2 Accumulated daily primary energy consumption (cool source group) of main module of absorption chiller/heater with auxiliary waste heat system recovery (absorption chiller/heater)(single and double combination) \(E_{ AC, ref, c, d }\)

The accumulated daily primary energy consumptions of the main modules of the following heat source models that are included in Form 7-3 “⑩ Name of air conditioning heat source group (cooling source) using waste heat, \(E_{ AC, ref, i }\) (Formula 2.1.98/ [5] p191), are outputted only in a period for operation of the main modules as a cool source system.

In the case where a heat storaging tank is included in “air conditioning heat source using waste heat, however, the accumulated daily primary energy consumption of the heat source group for additional operation is outputted in the same way mentioned above.

Table 61. Table of models and XMLs
Model	XML
Absorption chiller (steam)	AbcorptionChiller_Steam
Absorption chiller (cooling water changing discharge, steam)	AbcorptionChiller_Steam_CTVWV
Absorption chiller (hot water)	AbcorptionChiller_HotWater
Absorption chiller (single and double combination, city gas)	AbcorptionChiller_Combination_CityGas
Absorption chiller (single and double combination, cooling water changing discharge, city gas)	AbcorptionChiller_Combination_CityGas_CTVWV
Absorption chiller (single and double combination, LPG)	AbcorptionChiller_Combination_LPG
Absorption chiller (single and double combination, cooling water changing discharge, LPG)	AbcorptionChiller_Combination_LPG_CTVWV
Absorption chiller (single and double combination, steam)	AbcorptionChiller_Combination_Steam
Absorption chiller (single and double combination, cooling water changing discharge, steam)	AbcorptionChiller_Combination_Steam_CTVWV

G.10.3 Representative load factor of cool source group with absorption chiller/heater with auxiliary waste heat system recovery (absorption chiller/heater (single and double combination)), \(mxL_{ AC, ref, c, d}\)

The representative load factor in Form 7-3 “⑩ Name of air conditioning heat source group (cooling source) using waste heat,” \(mxL_{ AC, ref, i(m,n) }\) (Formula 2.1.91・Formula 2.1.93/ [5] p189), is outputted by day.

G.10.4 Accumulated daily primary energy consumption of main module of heat source group using waste heat, \(E_{ AC, ref, h, hr, d }\)

The accumulated daily primary energy consumption of the main module of a heat source group that is included in Form 7-3 “⑪ Name of air conditioning heat source group (heating source) using waste heat, \(E_{ AC, ref, i }\) (Formula 2.1.98/ [5] p191), are outputted only in a period for operation of the main module as a cool source system.

The primary energy consumptions of all pieces of heat source equipment in the subject heat source group, regardless of which fuel type is used, are accumulated.

G.10.5 Heat source load of heat source group using waste heat, \(q_{ AC, ref, h, hr, d }\)

The heat source load of a heat source group in Form 7-3 “⑪ Name of air conditioning heat source group (heating source) using waste heat, \(Q_{AC, ref, i, d }\) （Formula 2.1.86/ [5] p184), is outputted by day.

G.10.6 Primary energy consumption of hot-water supply system using waste heat, \(E_{ W, hr, d }\)

The annual primary energy consumption of a hot-water supply system of a water heater in Form 7-3 “⑫ Name of water heater using waste heat,” \(E_{ w }\) (Formula 2.4.1/ [5] p306), is divided by day. Each value after being divided is outputted.

The way of dividing the consumption each daily unit is the same as in the item of hot-water supply described in “ ① Accumulated daily power consumption (primary).”

G.10.7 Hot-water supply load of hot-water supply system in system available to waste heat, \(q_{ W, hr, d }\)

The annual hot-water supply load of a water heater in Form 7-3 “⑫ Name of water heater using waste heat,” \(Q_{ wr, i }\) (Formula 2.4.2/ [5] p306), is outputted by day.

G.10.8 Accumulated daily operation time of air conditioning (cool source group), \(T_{ AC, c, d }\)

There is an air conditioner group in Form 7-3 “⑩ Name of air conditioning heat source group (cool source)” that is designated as the name of a cool heat source in Form 2-7 (Air conditioning) air conditioner input sheet. The cooling operation time of the air conditioner group, \(T_{ AC, ahu, c, i, d }\) (Formula 2.1.57～61/ [5] p173), is outputted by day.

G.10.9 Accumulated daily operation time of air conditioning (heat source group), \(T_{ AC, h, d }\)

There is an air conditioner group in Form 7-3 “⑩ Name of air conditioning heat source group (heat source)” that is designated as the name of a cool heat source in Form 2-7 (Air conditioning) air conditioner input sheet. The heating operation time of the air conditioner group, \(T_{ AC, ahu, c, i, d }\) (Formula 2.1.62～64/p174), is outputted by day.

G.11 Way of calculating coefficient (difference in average power between operation and non-operation hours of building)

1) Obtain schedules for ① air conditioning operation, ② lighting heat generation and ③ equipment heat generation in room uses of a building to be calculated (matrix of 8760×1).
*Database to be used　ROOM_COND.csv
*The schedule for air conditioning operation (including decimals) that is larger than 0 or is o, is deemed to be “1” or to be “0,” respectively. Other schedules are allowed to have decimals.

2) Calculate a schedule for weighing floor areas at the following time t in room uses of a building to be calculated (matrix of 8760×1).

“Room where air conditioning is calculated,“ described in Form 1

\[Sawt_{ac}(t) = \sum (Air conditioning operation schedule at time t in room use of the relevant room \times Floor area of the relevant room)\]

Room where lighting is calculated,“ described in Form 1

\[Sawt_{ac}(t) = \sum (Lighting operation schedule at time t in room use of the relevant room \times Floor area of the relevant room)\]

All rooms described in Form 1

\[Sawt_{ac}(t) = \sum (Equipment heating schedule at time t in room use of the relevant room \times Floor area of the relevant room)\]

3) Using the above schedule at each time that was determined in the above section, calculate a ratio when an accumulated value at each day is 1(matrix of 8760×1).

\[rSawt_{ac}(t) = \begin{cases} 0 & , Sawdsum_{ac}(d) = 0 \\ \frac{ Sawt_{ac}(t) }{ Sawdsum_{ac}(d) } & , \mbox{Other} \end{cases}\]

\[rSawt_{lt}(t) = \begin{cases} 0 & , Sawdsum_{lt}(d) = 0 \\ \frac{ Sawt_{lt}(t) }{ Sawdsum_{lt}(d) } & , \mbox{other} \end{cases}\]

\[rSawt_{oa}(t) = \begin{cases} 0 & , Sawdsum_{oa}(d) = 0 \\ \frac{ Sawt_{oa}(t) }{ Sawdsum_{oa}(d) } & , \mbox{other} \end{cases}\]

Where,
\(Sawdsum _\{ac}(d)\): Accumulated value of \(Sawt_\{ac}(t)\) at date d (Accumulation of a value at 1:00 to 24:00 on each day)
\(Sawdsum _{lt}(d)\) : Accumulated value of \(Sawt_{lt}(t)\) at date d (Accumulation of a value at 1:00 to 24:00 on each day)
\(Sawdsum _\{oa}(d)\): Accumulated value of \(Sawt_\{oa}(t)\) at date d (Accumulation of a value at 1:00 to 24:00 on each day)

4) Calculate a power consumption at a time t on a date d in the whole building to be calculated (matrix of 8760×1).

\[\begin{eqnarray*} Et_{ele}(t) & = & Eac_{ele}(d) \times rSawt_{ac}(t) \\ & \quad & + \frac{ Ev_{ele}(d) }{ 24 } \\ & \quad & + Elt_{ele}(d) \times rSawt_{lt}(t) \\ & \quad & + \frac{ Ehw_{ele}(d) }{ 24 } \\ & \quad & + \frac{ Eev_{ele}(d) }{ 24 } \\ & \quad & + Eoa_{ele}(d) \times rSawt_{oa}(t) \end{eqnarray*}\]

Where,
\(Eac_\{ele}(d)\): Accumulated daily power consumption of air conditioning equipment at date d [MWh/day]
\(Ev_\{ele}(d)\): Accumulated daily power consumption of mechanical ventilation equipment at date d [MWh/day]
\(Elt_\{ele}(d)\): Accumulated daily power consumption of lighting installation at date d [MWh/day]
\(Ehw_\{ele}(d)\): Accumulated daily power consumption of hot-water supply system at date d [MWh/day]
\(Eev_\{ele}(d)\):　Accumulated daily power consumption of elevator at date d [MWh/day]
\(Eoa_\{ele}(d)\): Accumulated daily power consumption of other at date d [MWh/day]

5) Calculate a coefficient at a date d, \(f_\{eopeHi}(d) \).

\[Et_{ele,day}(d) = \sum_{t=7}^{20}Et_{ele}(t) - Epv_{ele}(d)　　　(Σ is an accumulated value from 7:00 to 20:00.)\]

\[Et_{ele,night}(d) = \sum_{t=1}^{6} ΣEt_{ele}(t)+ \sum_{t=21}^{24} ΣEt_{ele}(t) (Σ is an accumulated value from 1:00 to 6:00 and an accumulated value from 21:00 to 24:00.)\]

\[f_{eopeHi} (d) = \begin{cases} 1 & , Et_{ele,day}(d) = 0 \\ 100 & , Et_{ele,night}(d) = 0 \\ \frac{ Et_{ele,day}(d) }{ Et_{ele,night}(d) } & , \mbox{Other} \end{cases}\]

Where,
\(Epv_\{ele}(d)\) is an accumulated daily power generation of solar power system at date d [MWh/day].

\[1 \leqq f_{eopeHi} (d) \leqq 100\]

A range of the coefficient is as shown above.